“Uncertainty” is a concept that reflects imperfect or unknown information. It usually arises from imperfect measurements in environments that are only partially observable. Uncertainty also arises when predicting future events, where one can estimate the likelihood of something happening but cannot make a statement for certain.
Uncertainty for single predictions is increasingly important in machine learning and is often a requirement for clients. Especially when the consequences of a wrong prediction are high, you need to know what the probability distribution of an individual prediction is. To calculate this, usually, the Bayesian methods are immediately considered. But these methods also have their downsides. For example, they can be computationally expensive when dealing with large amounts of data or lots of parameters.
In this blog post, you can find the theory behind different types of uncertainty, as well as a Bayesian and a frequentist approach to analyze epistemic uncertainty. (You can also find the code used in this blog post on Yu R Tani’s Github.)
What are the types of uncertainty?
As mentioned earlier, the concept of uncertainty also shows up in machine learning models’ predictions. Like humans, a machine cannot predict a future event with absolute confidence. That said, machine learning models’ uncertainty can be of two kinds: aleatoric and epistemic. Bear in mind, though, that aleatoric and epistemic uncertainties are not rigid terminologies, and often depend on the context of the model and the problem at hand.
Join the leading data & AI consultancy in the Netherlands. Click here to view our vacancies
Aleatoric uncertainty
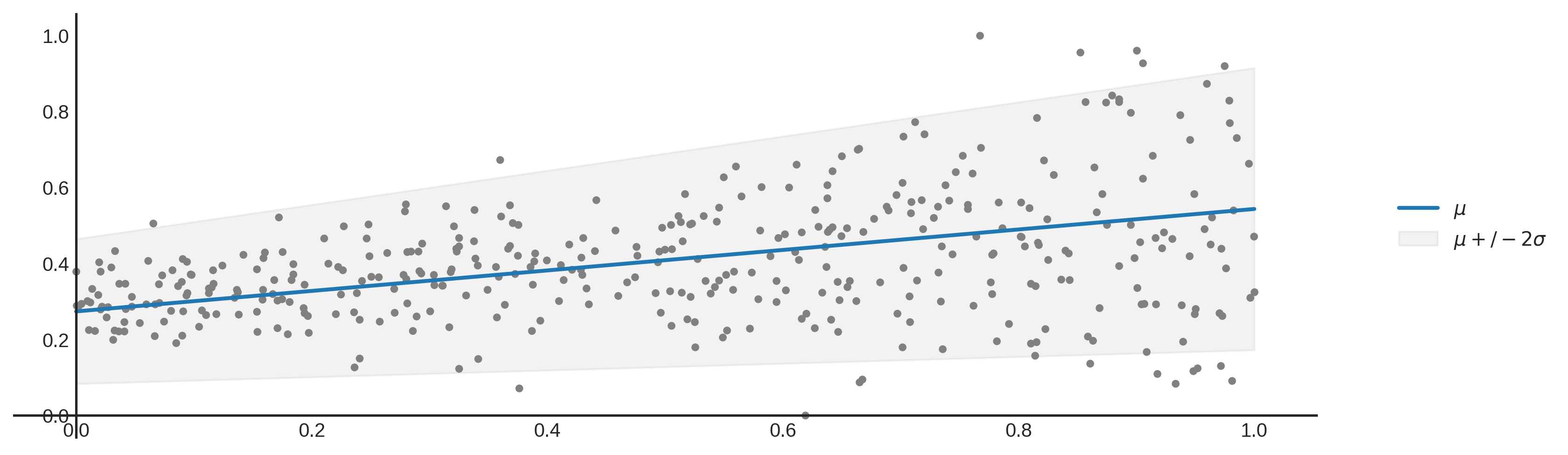
Aleatoric uncertainty is the kind of uncertainty that arises from the inherent variability and randomness in the processes being modeled. In other words, it is the “noise” in the data. For example, when predicting the weight of a person based on their height, you will still face some variability in the prediction even if you have a perfect model. In the plot below, the aleatoric uncertainty equals the mean plus or minus 2 times the standard deviation.
Epistemic uncertainty
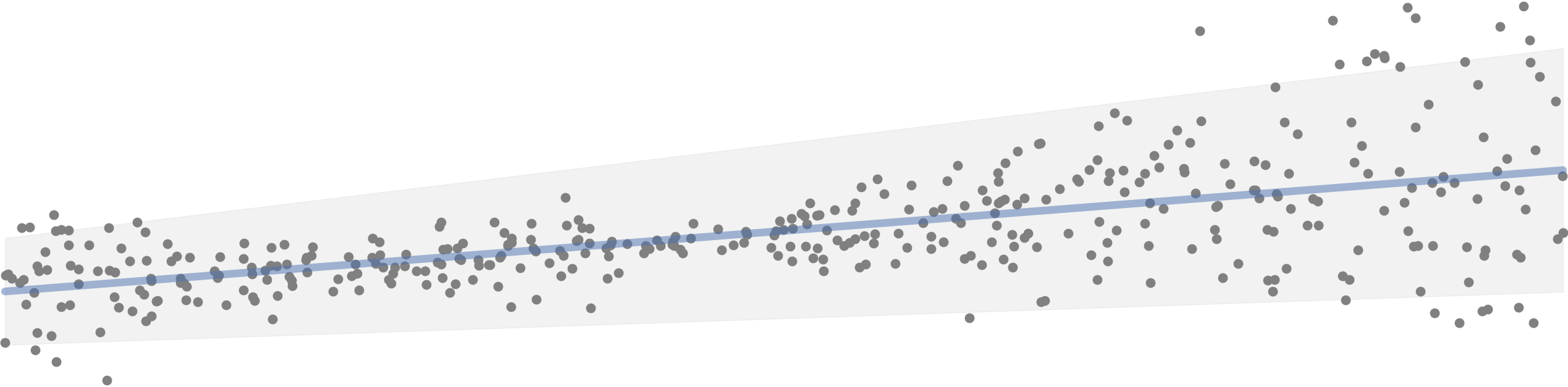
Epistemic uncertainty is the uncertainty originating from our lack of knowledge about the model or the values its parameters should have. For example, if you’re modeling a linear regression to predict stock prices based on historical data, but are uncertain about which features to use or even their coefficients, that is called epistemic uncertainty.
In the plot below, you can say that all blue lines fit the data reasonably well, but which one fits the data the best? Using linear models from sklearn for example, we can choose a model that performs best for a certain metric - global or local optimum.

Aleatoric uncertainty cannot be reduced but it can be identified and quantified, since it is inherent in the nature of the data and a fundamental part of the system being modeled. On the other hand, we can work around the epistemic uncertainty - for instance, it can be reduced with more data, or with an improved model.
Join Xomnia's Data & Drinks event about the latest trends in the world of AI. Click here.
How to deal with epistemic uncertainty?
1) Bayesian, the traditional way:
The Bayesian approach is particularly well-suited for dealing with epistemic uncertainty. In case you are not familiar with it, Bayesian statistics fundamentally interprets probability as the degree of belief in an event. This “degree of belief” may be based on prior knowledge originating from other experiments or on personal beliefs about the event.
There are some key components required in the Bayesian methodology:
- The prior distribution, which is the degree of belief before observing the data.
- The likelihood function represents the probability of observing the data given the model parameters.
- Posterior distribution, which is the updated probability distribution after taking into account the prior distribution and the observed data. The Bayes theorem calculates the posterior distribution by combining the prior distribution and the likelihood function.
As more data becomes available, the posterior distribution is updated. The posterior distribution from one analysis becomes the prior for the next analysis. That way, the epistemic uncertainty can be mitigated with the Bayesian approach by starting with prior information, constantly updating it with newly observed data, and continually refining beliefs about the model parameters. Additionally, the Bayesian approach can quantify parameter uncertainties. It is possible to explicitly quantify the uncertainty associated with parameter estimates because the posterior distributions provide ranges of plausible values for every model parameter.
Monte Carlo Dropout is a technique inspired by the Bayesian paradigm. It extends dropout, a regularization method in neural networks, to estimate model uncertainty. By applying dropout during both training and inference and running multiple stochastic forward passes, it generates an ensemble of models with different parameter settings. The variance across these predictions serves as a proxy for epistemic uncertainty, providing a measure of the model's uncertainty about its own predictions. Monte Carlo Dropout helps capture and quantify epistemic uncertainty, offering a valuable approach to improve model robustness and reliability.
However, there are cons to the Bayesian paradigm. Firstly, the prior distribution can be quite subjective, and different data scientists may have different opinions about appropriate priors. Also, this methodology can become very time-consuming and expensive computationally, particularly for more complex models and large datasets, not to mention the model interpretability: Bayesian results can be challenging to interpret and communicate, especially for non-experts.
2) Quantile regression: An alternative approach, borrowed from frequentist statistics
It is also possible to get insights into epistemic uncertainty with a frequentist technique, namely, quantile regression. For more context, the frequentist paradigm is a more traditional statistics methodology that focuses on objective probabilities based on repeated experiments. It emphasizes making inferences about a population based on the frequencies of observed examples and does not incorporate subjective beliefs or prior knowledge about parameters into inferences.
Even though the quantile regression technique does not address the epistemic uncertainty directly, it can be part of a broader approach. The quantile regression is a technique that estimates the relationship between variables at the mean but also various quantiles of the distribution, e.g. the median, and the lower and upper percentiles. With coefficient estimates for different quantiles, you can investigate the relationship between variables across the distribution; if variation is present, that can reflect uncertainty in the variable relationship.
Don't miss Xomnia's latest business cases and blogs. Subscribe to our newsletter.
But how to use quantile regression to understand epistemic uncertainty?
1) Firstly, conduct the quantile regression model to estimate the different quantiles of the response variable: This provides a comprehensive view of the distribution revealing more insight into the variability beyond the mean.
2) Explore the data dispersion: You can analyze the estimated quantiles to understand the data, as the spread of the quantiles can indicate the overall uncertainty in predictions. Additionally, the quantile regression is generally more reliable in the presence of uncertainties or outliers than the mean-based regression, and that is because quantile regression is less sensitive to extreme values.
3) Use the results to construct prediction intervals around the estimated quantiles: These intervals can provide a range of plausible values for the response variable.
4) Employ model averaging techniques: Instead of relying on a single quantile regression model, you can average predictions from multiple models or consider a range of quantiles to account for uncertainty in choosing the appropriate model structure.
Conclusion
Frequentist approaches do not explicitly model prior knowledge like Bayesian methods do. However, they can still provide insights into epistemic uncertainty through careful model selection, robust estimation techniques, and consideration of parameter estimation uncertainty. The frequentist paradigm is a convenient way to work around Bayesian’s complexity and lack of interpretability in some scenarios, but addressing the uncertainty more broadly may require borrowing concepts from the Bayesian approach. In the end, it depends on the data at hand and your personal choice and preference to understand the epistemic uncertainty from your model.